Divergent_Integral
Spastic ricecel, heightmogged by 99.74% of men
★★★★
- Joined
- Jul 3, 2020
- Posts
- 851
For your edification and intellectual stimulation I will post a math problem on here daily (or at least a few times a week). I will try to make the problems as accessible as possible, in that I will assume no really advanced mathematical knowledge. Just a bit of cleverness will do.
You may post your solutions in the thread. If none are received, I will give the solution myself the next day. Good luck, and happy problem solving!
Problem #0001
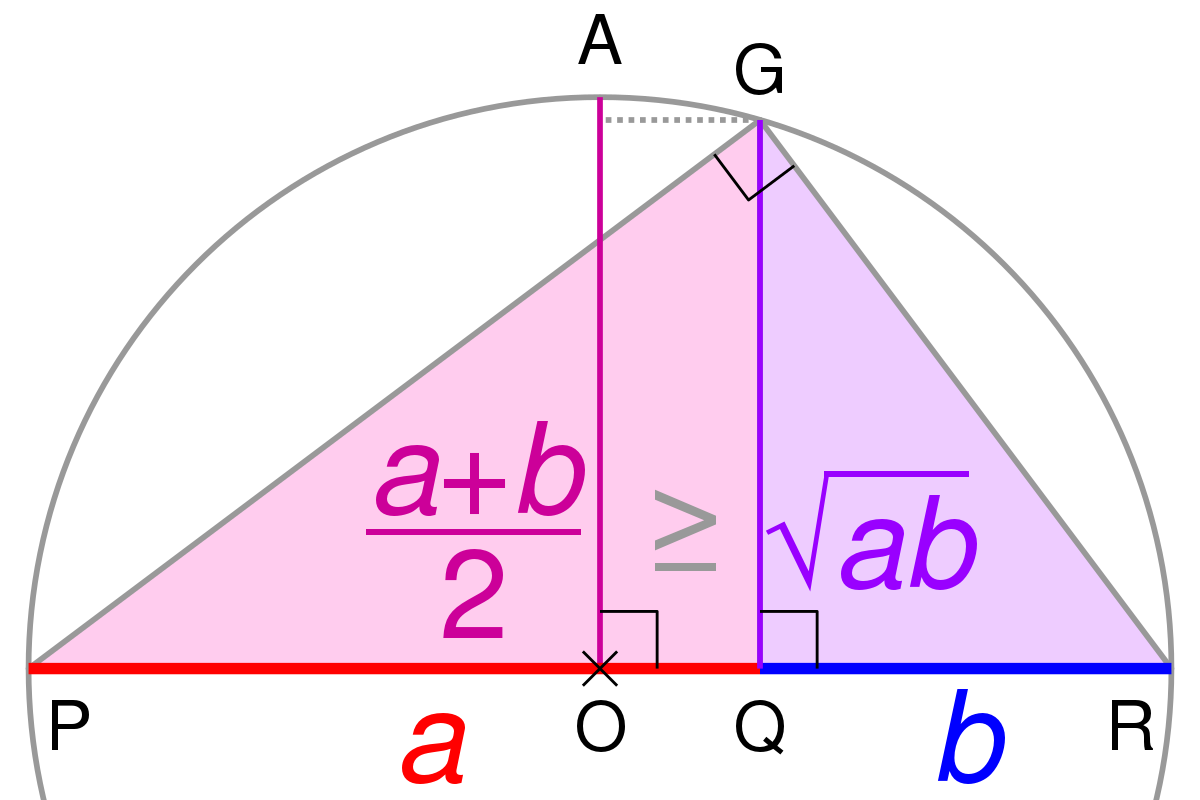
Let a, b, c be positive numbers such that a + b + c = 1. Prove that (1 - a)(1 - b)(1 - c) >= 8abc. Under what conditions on a, b, c does the equal sign hold?
You may post your solutions in the thread. If none are received, I will give the solution myself the next day. Good luck, and happy problem solving!
Problem #0001
Let a, b, c be positive numbers such that a + b + c = 1. Prove that (1 - a)(1 - b)(1 - c) >= 8abc. Under what conditions on a, b, c does the equal sign hold?