D
Deleted member 6657
blockhead
-
- Joined
- May 6, 2018
- Posts
- 3,910
stumped tbh ngl
12.56Problem #0004
View attachment 386812
In the diagram, KLJ is right angled at J, with JK=3 and JL=4.
KLJ is inscribed in a quarter circle with radius ML, as shown.
What is the area of the quarter circle?
@Diocel @grondilu @mental_out @SelfCrucified @your personality @Divergent_Integral
Have a marvelous day and happy problem solving.
5piProblem #0004
View attachment 386812
In the diagram, KLJ is right angled at J, with JK=3 and JL=4.
KLJ is inscribed in a quarter circle with radius ML, as shown.
What is the area of the quarter circle?
@Diocel @grondilu @mental_out @SelfCrucified @your personality @Divergent_Integral
Have a marvelous day and happy problem solving.
Yes. Thank you for this.
Can I share some problems as well?
Yes, that’s correct.
4πProblem #0004
View attachment 386812
In the diagram, KLJ is right angled at J, with JK=3 and JL=4.
KLJ is inscribed in a quarter circle with radius ML, as shown.
What is the area of the quarter circle?
@Diocel @grondilu @mental_out @SelfCrucified @your personality @Divergent_Integral
Have a marvelous day and happy problem solving.
Are the triangles KML and JKL congruent? I assumed it, but I'm not sure.This is an interesting one.
I think it can be solved by using the angle MLK as an unknown parameter x. Then you solve for the distance MJ to be 5 cos(x). The distance MJ is four times the sine of the angle MLJ, which is x plus the angle MLJ, which is known.
Will do tommorowYes, that’s correct.
Could you give me a brief outline of the method you used to arrive at that conclusion? I’d love to know, since I only have two different solutions I plan on presenting tomorrow
Nah don't pay attention to what I wrote, I was trying to be quick but I ended up writing something wrong.Are the triangles KML and JKL congruent? I assumed it, but I'm not sure.
Is the solution supposed to be that complex? Wow.I used Mathematica, ngl.
View attachment 387059
Probably not. This is kind of the brute force approach, I'm sure there is a shortcut somehow.Is the solution supposed to be that complex? Wow.
How do you figure this?Then the squared diameter is (5+3)² + 4² = 64 + 16 = 80
I have considered this but still I cannot find a way to determine the length of the radius.Hint for problem #0004
Try looking at isosceles JML
L'K = KL, and KL = 5 by hypothesis, so L'K = 5.How do you figure this?
Beautiful solution, well done! I did not solve the problem this way, but this is brilliant. Kudos to you, man.Oh I think I see the smarter way to do it.
Guys, next time you propose a geometry problem, I suggest you name your points with letters A, E, R, J, F, L, N, G, H, T, B and make it so the demonstration involves segments ER, AF, or triangles TBH, JFL and NGLWe can consider the whole circle and the point L' with whom L forms a diameter. Then everything is much simpler, especially since L', K and J are aligned (not obvious, but probably not difficult to prove either)
Then the squared diameter is (5+3)² + 4² = 64 + 16 = 80. We can divide by 4 to get the squared radius, which gives 20, and by four again and multiply by pi to get the quarter of the disk area. This gives 5pi.
PS. To prove that L', K and J are aligned, we just need to see that the triangle L'JL is right-angled in J because this angle intercepts a diameter. Thus the line L'J is orthogonal to JL, and since KJ is orthogonal to JL too, these lines are the same because by one point only one line can intersect an other line with a right angle (Euclide's axiom).
One of my solutions involves the cosine addition identity. Namely cos(a+b)=cos(a)cos(b)-sin(a)sin(b).How do you figure this?
I have considered this but still I cannot find a way to determine the length of the radius.
I'm looking forward to itAlso, I will totally use segments ER, AF and triangles TBH, JFL. Even maybe quadrilateral GOER next tme.
First, this is not an IQ mog thread. This is simply a thread where incels who enjoy racking their brain on a challenging math problem can come together and do so.Why this IQ mog thread was pinned?
@Divergent_Integral @WorldYamataizer, why aren't you studymaxxxing so that you can betamaxxx later?
You have hopes, unlike braindead cels like me.
Ewwww sounds bittersweet, but at least you are being educated and doing something with your lifetime unlike rotting neets like me who can't study in uni.First, this is not an IQ mog thread. This is simply a thread where incels who enjoy racking their brain on a challenging math problem can come together and do so.
I assure you none of us here were gifted with an “extraordinary talent in mathematics” as I was unable to solve problem #0003, and I stumped a few users with #0004. We just like a challenging puzzle!
Maybe mods pinned it because this thread will be thriving for a while? Not sure about that. I am studymaxxing btw. I’m going into my first year of Uni this fall for math. Im. ot planning on betabux. I just have to get my degree so my rice parents can have “peace of mind” then I can move on with my life.
Misery loves company! Dw brocel, everyone here on .co got ur back. I hope you find some really sweet, zen copes.Ewwww sounds bittersweet, but at least you are being educated and doing something with your lifetime unlike rotting neets like me who can't study in uni.
Still mogs me
Problem #0004
View attachment 386812
In the diagram, KLJ is right angled at J, with JK=3 and JL=4.
KLJ is inscribed in a quarter circle with radius ML, as shown.
What is the area of the quarter circle?
@Diocel @grondilu @mental_out @SelfCrucified @your personality @Divergent_Integral
Have a marvelous day and happy problem solving.
more efficient to tie your shoe off the walkwayI was recently at an international airport, trying to get from one end of a very long terminal to another. It inspired in me the following simple maths puzzle, which I thought I would share here:
Suppose you are trying to get from one end A of a terminal to the other end B. (For simplicity, assume the terminal is a one-dimensional line segment.) Some portions of the terminal have moving walkways (in both directions); other portions do not. Your walking speed is a constant, but while on a walkway, it is boosted by the speed of the walkway for a net speed of
of the walkway for a net speed of . (Obviously, given a choice, one would only take those walkways that are going in the direction one wishes to travel in.) Your objective is to get from A to B in the shortest time possible.
. (Obviously, given a choice, one would only take those walkways that are going in the direction one wishes to travel in.) Your objective is to get from A to B in the shortest time possible.
- Suppose you need to pause for some period of time, say to tie your shoe. Is it more efficient to do so while on a walkway, or off the walkway? Assume the period of time required is the same in both cases.
- Suppose you have a limited amount of energy available to run and increase your speed to a higher quantity
(or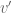 , if you are on a walkway). Is it more efficient to run while on a walkway, or off the walkway? Assume that the energy expenditure is the same in both cases.
, if you are on a walkway). Is it more efficient to run while on a walkway, or off the walkway? Assume that the energy expenditure is the same in both cases.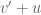
Efficient to do it on the walkway.
- Suppose you need to pause for some period of time, say to tie your shoe. Is it more efficient to do so while on a walkway, or off the walkway? Assume the period of time required is the same in both cases.
it is lelThis isn't math tbh.
the second one is tbhit is lel
first can be answered on a mathematical level and on phically intuitive levelthe second one is tbh
not the first.
Assuming time of sprint is constant t1, distances for walkway is (u + v') * t1 and distance for non walkway is v' * t1 WLOGSuppose you have a limited amount of energy available to run and increase your speed to a higher quantity(or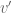 , if you are on a walkway). Is it more efficient to run while on a walkway, or off the walkway? Assume that the energy expenditure is the same in both cases.
, if you are on a walkway). Is it more efficient to run while on a walkway, or off the walkway? Assume that the energy expenditure is the same in both cases.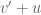
Even the second is less but still intuitive tbhfirst can be answered on a mathematical level and on phically intuitive level
Are you asking this ?At which times during the day do the hour and minute hands of an ordinary analog clock make exactly equally sized angles on both sides of the vertical line joining the 12h and 6h marks? Give your answer to the nearest second. You may assume that both hands move at a perfectly continuous rate, in such a way that every time the minute hand hits the 12h mark, the hour hand exactly hits an hour mark.
I said both sides of the line. So like 1:50, but more precisely.time of sprint in walkway = (v' / v) * t1 + t1
time of sprint in non-walkway = ((u + v')/(u+v)) * t1 + t1
Obviously 2nd one is lower time
Even the second is less but still intuitive tbh
Like if you think of v' is infinity/very high or u is infinity/very high
It would obviously be useful to use the "teleport" to skip the walking (v' is high)
Or it would be obvious to speed up while walking, rather than "teleport" (u is high)
Are you asking this ?
View attachment 387380
if so then timing is h,m
and the equation is h/12 + m/60 = (30-m)/60
h = 0,1,2,3...11
then it will be : h/12 + m/60 = 1 - m/60I said both sides of the line. So like 1:50, but more precisely.
Our best representative went ER before going ER was even a thing :Mathematicians on the forum? Wtf is wrong with society
Holy fuck that is complex as shit
Also made a retarded error in this lolthen it will be : h/12 + m/60 = 1 - m/60
h = 0,1,2,3...11
Yeah I may have made it look more complex than necessary.Holy fuck that is complex as shit
I am very pleased with this second solution of yours.





