says the nigga with an anime pfp and 14k posts in under a year
14k+63k
Now that you're in the math thread you might as well complete the addition
What is (N)+o x S^ex = in^kwell
Evalute the summation of (n!)²/(2n)! from n = 1 to infinity
He's back! Lifefuel
Anyway, here's a rather labor-intensive way of evaluating the sum:
where the equality with a T uses Tonelli's theorem and the equality with a D uses the differentiation theorem for power series.
French fries @trying to ascend
We need a physics thread.
You could start one?
C
This thread needs more elementary geometry, here's a simple problem I think the majority of people would be able to approach:
Construct equilateral triangle ABC, it's incircle (O) has radius of 1. From here we can construct three infinite sequences of circles, each circle is tangent to the two sides of the triangle as well as the previous circle (as pictured). Calculate the sum of the circumferences of all circles
Construct equilateral triangle ABC, it's incircle (O) has radius of 1. From here we can construct three infinite sequences of circles, each circle is tangent to the two sides of the triangle as well as the previous circle (as pictured). Calculate the sum of the circumferences of all circles
Too low IQ to start one.
brutal
This thread needs more elementary geometry, here's a simple problem I think the majority of people would be able to approach:
Construct equilateral triangle ABC, it's incircle (O) has radius of 1. From here we can construct three infinite sequences of circles, each circle is tangent to the two sides of the triangle as well as the previous circle (as pictured). Calculate the sum of the circumferences of all circles
Since the sum of the circumferences is proportional to the sum of the diameters, all we have to do is calculate the sum of the diameters and multiply by pi. As regards the sum of diameters, it's evident from the picture (and the fact that the inradius is 1) that (sum of diameters) + 1 = 3*circumradius. Since the inradius is 1, we may deduce that circumradius = 2*inradius = 2*1 = 2, so the sum of diameters = 3*2 - 1 = 5. Ergo, the final answer should be 5*pi.
i got the same final answer, but your solution is more elegant than mine. i inscribed the incircle in a regular hexagon to notice that the radius of the three circles is one third the radius of the previous one. so i calculated the infinite geometric sum
2pi+3\sum_{n=1}^\infty 2pi(1/3)^n
That's still pretty elegant (and arguably more rigorous than my solution).
You can post those problems here as well, I've posted some in the past, but no one tried to solve them
Here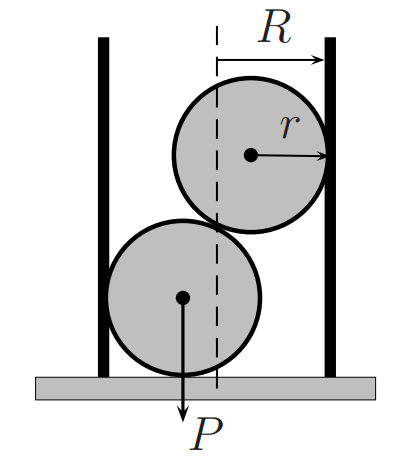
r = 3/4R.
P = weight of each sphere.
Find the value of the weight of the cylinder, such that the system is at rest
Prove the following identities
this video is well worth watching and explains a very nice combinatorial method for tackling alternating sums
I took the problems from this video btw. I managed to solve them myself after watching the video, so I'm sure you guys can too.
I took the problems from this video btw. I managed to solve them myself after watching the video, so I'm sure you guys can too.
Wow, you guys are amazing to be honest
A expansion of numbers
For example
If you do
(0+1)^2
It will be
(0+1)(0+1)
00 +01 +10+11
Which will be
0+1+2+3 in binary
Same for
(0+1)^3
Which will be sum of 0 to 8 in binary
If we neglect the actual meaning of + sign for a moment and reconsider it after expansion can we say that
(0+1+2+3+4+5+6+7+8+9)^2
Is just the sum from 0 to 99
If you concatenate instead of multiplying. Your observation on binary is very closely related to the fact that the sums of rows of Pascal's triangle add up to powers of 2.
A expansion of numbers
For example
If you do
(0+1)^2
It will be
(0+1)(0+1)
00 +01 +10+11
Which will be
0+1+2+3 in binary
Same for
(0+1)^3
Which will be sum of 0 to 8 in binary
If we neglect the actual meaning of + sign for a moment and reconsider it after expansion can we say that
(0+1+2+3+4+5+6+7+8+9)^2
Is just the sum from 0 to 99
Wow. A question that even someone like me can solve lolThis thread needs more elementary geometry, here's a simple problem I think the majority of people would be able to approach:
Construct equilateral triangle ABC, it's incircle (O) has radius of 1. From here we can construct three infinite sequences of circles, each circle is tangent to the two sides of the triangle as well as the previous circle (as pictured). Calculate the sum of the circumferences of all circles
If
AB=C
If A is a mxn matrix
Find a generalised nxn matrix B such that
The sum of elements of each row of A and C are equal
AB=C
If A is a mxn matrix
Find a generalised nxn matrix B such that
The sum of elements of each row of A and C are equal
What do you mean by "a generalised nxn matrix"? Can't I just take B to be the identity matrix?
No ,the entries of b should depend on n
Math
Both, but mostly invented, of course. Math is not Science. Tweaking things and seeing how they work and making them work can (mostly) be done without a lot of maths. Even complex Maths is just a useful language to help us find reference points and reproduce results more quickly. However, otherwise, all the "big long math equations" to solve "the big questions about muh fabric of reality" are mostly bullshit and a waste of time.
I think you're grossly underselling maths here. First off, I can't even imagine a world without arithmetic (a bona fide part of maths) and I doubt you can either. Computers are essentially math machines and they're pretty indispensable these days. And then there's engineering -- good luck building a giant bridge or flat without being able to calculate whether the support beams will hold beforehand.
Tfw i need to know shortest distance between two lines to make graphics work
I'm definitely not. Science is not Math. Engineering is like a craft. Math is like manuel labor. I once thought the same about math pivotal role in everything, in Truths. Figuring out how Engineering & Physics play out in the real world doesn't need a lot of mathematical dick measuring to work. I'm talking about all the theoretical mathematics of never ending masturbatory bullshit.
I was not talking about workable geometry or arithmetic up to calculus. And I am not talking about quantum computing for necessary function. I'm talking about all the math which gets thrown into a useless Cosmology and Astrophysics dick measuring contest which people then call "Big Science"
Last edited:
I figured as much. Still, just because large swaths of math are (currently) useless doesn't mean math as a whole is useless. You made it come across that way (at least to me). Every academic discipline has its useless outgrowths, math is no exception of course. I think we're in agreement despite having differing mental images of math.
Maths, in theoretical physics, because of the enormous amount of fake credit given to it by theoretical Science TV presenters has also become almost "useless" in the sense that it's being used less to solve real problems. This is what I feel is the case.
While I'm not a theoretical phycisist, I think the focus of theoretical physics is mostly "useless" these days. Things like quantum gravity and cosmology are just not all that useful in everyday life. To me it seems the problem you highlight here is less about math and more about physics.
Given a^2 + b^2 + c^2 = 3, prove a^3 * b + b^3 * c + c^3 * a <= 3
Hey, welcome to the forum! Strong first post (unironically).
I'm honestly stumped. I tried Cauchy-Schwarz in conjunction with the AM-GM ineq., I tried Lagrange multipliers, I tried spherical coordinates -- I can't get any of them to work. Got a hint?
I tried all that shit too. Idk the answer, I just saw this problem somewhere. Apparently its a very strict inequality as well: for the cyclic sum of a^(2 + x) * b^(2 - x) on x in [0, 2], x = 1 is the maximum value at which it is never greater than 3 (tested using a python script).
The latest approach i tried was (a^2 + b^2 + c^2)^2 - (3 * cyclic sum of(a^3 *b)) >= 0, which gave this equation:
a^2 * (3b - 2a)^2 + b^2 * (3c - 2b)^2 + c^2 * (3a - 2c)^2 >= a^2 * b^2 + b^2 * c^2 + c^2 * a^2
Idk if anything can be done with this form. If you could get some help from other people to do this that would be nice too.
I tried some more, but still couldn't figure it out. Then I went the internet for answers and found this:
chứng minh :$(a^2+b^2+c^2)^2\geq 3(a^3b+b^3c+c^3a)$ - Bất đẳng thức và cực trị
chứng minh :$(a^2+b^2+c^2)^2\geq 3(a^3b+b^3c+c^3a)$ - posted in Bất đẳng thức và cực trị: chứng minh :$(a^2+b^2+c^2)^2\geq 3(a^3b+b^3c+c^3a)$ với a,b,c >0 cho a,b,c>0.CM :$\dfrac{a^3}{b^2-bc+c^2}+\dfrac{b^3}{a^2-ac+c^2}+\dfrac{c^3}{a^2-ab+b^2}\geq a+b+c$
BasedI tried some more, but still couldn't figure it out. Then I went the internet for answers and found this:
crazychứng minh :$(a^2+b^2+c^2)^2\geq 3(a^3b+b^3c+c^3a)$ - Bất đẳng thức và cực trị
chứng minh :$(a^2+b^2+c^2)^2\geq 3(a^3b+b^3c+c^3a)$ - posted in Bất đẳng thức và cực trị: chứng minh :$(a^2+b^2+c^2)^2\geq 3(a^3b+b^3c+c^3a)$ với a,b,c >0 cho a,b,c>0.CM :$\dfrac{a^3}{b^2-bc+c^2}+\dfrac{b^3}{a^2-ac+c^2}+\dfrac{c^3}{a^2-ab+b^2}\geq a+b+c$diendantoanhoc.org
In d dimensional space, a set of unit vectors has the property that every pair forms an obtuse angle with the origin. Prove that there are at most d+1 vectors in the set.
Since it's obviously true for d = 1 and d = 2, I only have to really prove the induction step.
First, I'll show that the max in R^d is the same as the max for { x ∈ R^(d+1) | x_0 ⩽ 0 }. Since { x ∈ R^(d+1) | x_0 = 0 } ⊂ { x ∈ R^(d+1) | x_0 ⩽ 0 }, the max for the half-space is at least as big as the max for R^d. To see that it cannot exceed the max for R^d, it suffices to project onto { x ∈ R^(d+1) | x_0 = 0 }. Indeed, the unit vectors having an obtuse angle is equivalent to their inner product being negative, and since the x_0 component of the inner product is always negative * negative = positive, our projection will only make the inner product even more negative.
All that remains to be shown is that the max for R^(d+1) is exactly one greater than the max for { x ∈ R^(d+1) | x_0 ⩽ 0 }. Since we can always add e_0 (the unit vector in the positive x_0 direction) to a maximal set in the half-space, it's at least one greater. To see that we cannot add two (or more) vectors, suppose to the contrary that we have a set of at least the half-space max + 2 unit vectors in R^(d+1). Picking any one of these vectors and calling it v, none of the other vectors will be on the same side of the orthogonal complement of v (which the hyperplane perpendicular to v passing through the origin) because they are "obtusely related" to v. Doing a rotation such that v goes to e_0 would thus mean that we've jammed at least half-space max + 1 obtusely related vectors into the half-space -- contradiction.
Nice problem. Feel free to keep 'em coming.
Slight correction: in the first part the inequality should be strictly less than 0. Any valid set in R^d can be projected into this half space by adding x_0 = -epislon for some significantly small epsilon that will preserve the obtuseness of the set.
Prove that if a graph on n vertices contains at least floor(n^2 / 4) edges and at least 1 odd cycle, it contains a triangle.
Yeah, you're right. My bad. I had come up with this, but forgot to implement it when I started writing. Here's a corrected version for completeness (changes in red).
Since it's obviously true for d = 1 and d = 2, I only have to really prove the induction step.
First, I'll show that the max in R^d is the same as the max for { x ∈ R^(d+1) | x_0 ⩽ 0 }. Since { x ∈ R^(d+1) | x_0 = 0 } ⊂ { x ∈ R^(d+1) | x_0 ⩽ 0 }, the max for the half-space is at least as big as the max for R^d. To see that it cannot exceed the max for R^d, it suffices to project onto { x ∈ R^(d+1) | x_0 = 0 }. Indeed, the unit vectors having an obtuse angle is equivalent to their inner product being negative, and since the x_0 component of the inner product is always negative * negative = positive, our projection will only make the inner product even more negative.
Since { x ∈ R^(d+1) | x_0 < 0 } ⊂ { x ∈ R^(d+1) | x_0 ⩽ 0 }, any "obtuse set" of unit vectors in the strict half-space is automatically one in the half-space. Conversely, since "obtusely related" vectors must have strictly negative inner product, making any zerovalent x_0 component ever so slightly negative will increase the negative inner product by an arbitrarily small positive amount. By choosing the now negative x_0 components small enough we can thus preserve all the negative inner products and transform any obtuse set of unit vectors in the half-space to one in the strict half-space. Ergo, the max for both half-spaces is the same.
All that remains to be shown is that the max for R^(d+1) is exactly one greater than the max for { x ∈ R^(d+1) | x_0 < 0 }. Since we can always add e_0 (the unit vector in the positive x_0 direction) to a maximal set in the half-space, it's at least one greater. To see that we cannot add two (or more) vectors, suppose to the contrary that we have a set of at least the half-space max + 2 unit vectors in R^(d+1). Picking any one of these vectors and calling it v, none of the other vectors will be on the same side of the orthogonal complement of v (which the hyperplane perpendicular to v passing through the origin) because they are "obtusely related" to v. Doing a rotation such that v goes to e_0 would thus mean that we've jammed at least half-space max + 1 obtusely related vectors into the half-space -- contradiction.
Last edited:
I'll sketch a proof using Mantel's theorem.
Suppose to the contrary that you have a graph w/o triangles. By Mantel's theorem, the graph must have ⩽ n^2 / 4 edges. This can be proved by inductively removing an edge (see e.g. here). If the number of edges is < n^2 / 4 we're done, so suppose that it has exactly floor(n^2 / 4) edges. It's not too difficult to deduce that such a graph must be a (balanced) bipartite graph from inductively removing edges again. However, bipartite graphs have no odd cycles.
Is there a way to prove this without Mantel's theorem?
This is the same as my approach, although I did not know that Mantels theorem had a name.
Given a set of points in R^d, every subset of d+1 points can be covered by a ball of radius 1. Prove that the entire set can be covered by a ball of radius 1.
I'm out of things to suggest for now, would be nice if you suggest the next thing.
Last edited:
Man, your problems ain't easy.
Let A be the given set in R^d. Let X_a be the unit ball centered at a ∈ A. Then the intersection of any d+1 elements of { X_a } contains the center of the ball that contains all d+1 a's. In particular, the intersection of any d+1 elements of { X_a } is nonempty, so the intersection of the whole of { X_a } is nonempty by Helly's theorem. Any point in the nonempty intersection of { X_a } is the center of a unit ball that contains all of A.
Is there a less overkill way to do this that you're familiar with?
I did not know Helly's theorem had a specific name, and my solution involved deriving Helly's theorem for the specific case of balls. I used induction on n starting with d+1 points and proved that if there is an intersection I_n for the balls centered around the first n points, X_n+1 must intersect I_n because the intersections between X_n+1 and the previous balls can not be disjoint (by the problem statement). I think this argument applies for any Lesbegue measure.
Prove that { sqrt(n) : n positive squarefree } is linearly independent over Q.
I'm not so sure it's that straightforward. Let's say we have four unit balls B_1 thru B_4 in R^2. We know that B_1 ∩ B_2 ∩ B_4 and B_2 ∩ B_3 ∩ B_4 and B_3 ∩ B_1 ∩ B_4 are nonempty, but what guarantees us that the intersection of all four is nonempty?
What does the Lebesgue measure have to do with this?
You are right, I had a flaw in the argument in my notes. The convexity of the balls is necessary to prove that potentially disjoint sets of intersection overlap.
This is equivalent to proving that Q(sqrt(p_1), ... , sqrt(p_m)) does not contain Q(sqrt(p_m+1)) as a subfield. By galois theorem, the subfields correspond to the group (C_2)^m and none of these subfields contain Q(sqrt(p_m+1)), so the proof is done. Actually proving galois theorem is hard.
Let X be a probability distribution of bounded vectors in R^d, and let X_1, X_2, and X_3 be 3 random independent vectors from X, and r is an arbitrary nonnegative real. Prove 2 * probability(norm(X_1 + X_2) >= r) >= (probability(norm(X_3) >= r))^2
sorry but I don't follow
Similar threads
RageFuel
Florida: 150 Men Arrested for Trying to Have Sex with Prostitutes in “Human Trafficking” Bust
- Shaktiman
- The Lounge
TheCatMan
Users who are viewing this thread
